j’ai tout essayé en croisant dans tous les sens mais je ne trouve jamais la réponse
Met les declareà la benne, ils ne servent à rien ici.
p1=(["_MIN"]=2 ["_MAX"]=20 ["_POIDS"]=0.5 ['trouvee']=false)
p2=(["_MIN"]=5 ["_MAX"]=10000000 ["_POIDS"]=0.5 ['trouvee']=false)
P=(${p1[@]} ${p2[@]})
echo ${P[@]}
20 2 false 0.5 10000000 5 false 0.5
salut
j’avais essayé ton script
chez moi il ne donne pas le même résultat :
avec bash : false false
avec ksh : 20 2 0.5 false 10000000 5 0.5 false
Merci mais ne vous cassez pas la tête avec l’implémentation en python ou avec des tableaux en bash (ou perl…), ces interpréteurs ne sont pas disponibles dans l’environnement cible. L’implémentation sera soit en script shell compatible POSIX pour l’interpréteur de commande ash de busybox, qui ne supporte pas les tableaux, soit en langage compilé type C.
J’ai modifié l’algorithme proposé par @dindoun pour prendre en compte le fait que l’application des minima n’est pas définitive et a lieu avant l’application des maxima. Je ne l’ai pas encore implémenté ni testé, dites-moi si vous voyez des erreurs ou des améliorations possibles.
EnsI = { 1..N }
EnsMin = { }
EnsMax = { }
# recherche des quantités fixes
pour i dans EnsI tel que Min[i] = Max[i] ou P[i] = 0
Q[i] = Min[i]
Qt = Qt - Min[i]
EnsMax = EnsMax + i
EnsI = EnsI - i
BOUCLE1:
# recherche des minima (provisoires)
EnsI = EnsI + EnsMin
EnsMin = { }
Qmin = 0
BOUCLE2:
Q = Qt - Qmin
si Q < 0
erreur : quantité totale insuffisante
Pt = somme(P[i] pour i dans EnsI)
pour i dans EnsI tel que Q * P[i] / Pt < Min[i]
Q[i] = Min[i]
Qmin = Qmin + Min[i]
EnsMin = EnsMin + i
EnsI = EnsI - i
goto BOUCLE2
# recherche des maxima (définitifs)
Pt = somme(P[i] pour i dans EnsI)
pour i dans EnsI tel que Q * P[i] / Pt >= Max[i]
Q[i] = Max[i]
Qt = Qt - Max[i]
EnsMax = EnsMax + i
EnsI = EnsI - i
goto BOUCLE1
pour i dans EnsI
Q[i] = Q * P[i] / Pt
Notes :
-
L’ensemble EnsMax ne sert à rien pour l’algorithme mais c’est pour la clarté.
-
Le « goto » à la fin des boucles « pour » n’est exécuté qu’une fois après avoir traité tous les éléments de l’ensemble EnsI.
salut
j’ai du mal avec tes notations; quitte à faire un algorithme en français, un dia serait plus facile à suivre
- tu devrais mettre un FIN DE BOUCLE
- dans boucle 1 , EnsI = EnsI + EnsMin rend inutile EnsI = EnsI - i de la la boucle précédente, non? Et alors la condition P[i]=0 est comprise dans Q * P[i] / Pt < Min[i]
Tu pourrais donc probablement mettre
pour i dans EnsI tel que Q * P[i] / Pt < Min[i] OU Min[i] = Max[i] ou P[i] = 0
Qu’est-ce que c’est ?
En fait BOUCLE1 et BOUCLE2 sont de simples étiquettes de goto, j’aurais pu mettre d’autres noms. Ou faire de vraies boucles « tant que ».
Je regarderai l’autre remarque à tête reposée.
Je ne vois pas pourquoi, non. Initialement EnsMin est vide au début de la première itération de BOUCLE1.
+ Correction de l’algorithme, il manquait le recalcul de la somme des poids après la recherche des minima
L’approche de l’algorithme précédent n’est pas satisfaisante, le résultat n’est pas toujours optimal ou cohérent.
J’ai suivi une autre approche qui me semble meilleure :
EnsP = { 1..N } # ensemble des quantités pondérées/non bornées
EnsFixe = { } # ensemble des quantités fixes
EnsMin = { } # ensemble des quantités bornées par min
EnsMax = { } # ensemble des quantités bornées par max
# calcul poids total des quantités non bornées
fonction P() = somme(P[i] pour i dans EnsP)
# calcul quantité disponible pour les quantités non bornées
fonction Q() = Qt - somme(Min[i] pour i dans EnsMin + EnsFixe) - somme(Max[i] pour i dans EnsMax)
# calcul ratio quantité disponible / poids total non borné
fonction R() = Q() / P()
# recherche des quantités fixes
pour i dans EnsP tel que Min[i] >= Max[i] ou P[i] <= 0
EnsFixe = EnsFixe + { i }
EnsP = EnsP - { i }
si Q() < 0
erreur : quantité insuffisante pour les minima
si EnsP != { }
# calcul des ratios min et max pondérés (attention si division entière)
pour i dans EnsP
Rmin[i] = Min[i] / P[i]
Rmax[i] = Max[i] / P[i]
fin = faux
tant que fin = faux
MaxRmin = plus grand Rmin[i] pour i dans EnsMin
MinRmax = plus petit Rmax[j] pour j dans EnsMin
si R() > MinRmax ou R() < MaxRmin
si MaxRmin - R() < R() - MinRmax
EnsMax = EnsMax + { j }
EnsP = EnsP - { j }
si EnsP = { }
fin = vrai # toutes les quantités sont bornées
sinon
EnsMin = EnsMin + { i }
EnsP = EnsP - { i }
si Q() < 0
fin = vrai
erreur : quantité insuffisante pour les minima
sinon
fin = vrai # toutes les quantités restantes sont entre min et max
pour i dans EnsP
Q[i] = Q() * P[i] / P()
pour i dans EnsMin + EnsFixe
Q[i] = Min[i]
pour i dans EnsMax
Q[i] = Max[i]
Je l’ai implémenté en bash (avec des tableaux) pour tester, les résultats de mes premiers tests sont prometteurs.
Une alternative serait peut être de mettre une granulométrie dans ta mémoire (paquet de 1G ou de 500M par exemple) ce qui est proche de la réalité, et une fonction qui à partir des tableau Q, Qmin et Qmax à un instant donné, te donne celui qui recevant le bloc te rapproche de la répartition optimale (un algorithme glouton donc). Tout repose sur cette fonction. Si les Qmin ne sont pas atteint elle fournit le i avec Q[i] le plus éloigné de son Qmin, puis ensuite le i tel que le rapport P[i]/P()-Q[i]/Q() soit le plus grand. À voir si ça marche bien. Cette fonction doit pouvoir être améliorée…
[j’ai essayé de trouver un truc radicalement différent de ton approche et avec une complexité fixe]
Tu veux dire une granularité ?
Si je comprends bien, tu suggères de répartir les grains entre les quantités en attribuant séquentiellement chaque grain à la quantité qui en a le plus besoin ? Déjà il me semble qu’on peut attribuer directement à chaque quantité le nombre de grains correspondant à son minimum et commencer la répartition à partir de là. C’est ce que fait l’algorithme de partman-auto. Concernant la fonction d’optimisation, effectivement tout repose sur elle. Comment savoir s’il vaut mieux optimiser P[i]/P() - Q[i]/Q() ou Q[i]/P[i] - Q()/P() ou encore une autre expression ?
Oui, granularité (va savoir ce qui s’est passé dans ma tête…)
Pour la remarque, oui bien sûr puisque ça va arriver à cette situation. Pour l’attribution de Qmin au démarrage, j’aime bien ne pas voir ça en deux étapes et tout mettre sur la fonction, c’est tout, mais ça ne change rien. Pour ta dernière question, il faut tester, il y a d’autres fonctions surement. À la louche P[i]/P()-Q[i]/Qt (et non Q()) me parait pas mal mais favorise les grosses partitions. Tu peux aussi plus simplement prendre le i réalisant le minimum de P[i]/Q[i] qui n’aura pas cet inconvénient.
Mais tu est obligé d’introduire un test supplémentaire dans la partie itérative, donc tu as de facto deux étapes : avant que tous les minima soient atteints et après.
Tu veux dire le maximum de P[i]/Q[i] (qui ne peut que diminuer en ajoutant des grains, ou le minimum de Q[i]/P[i] qui ne peut qu’augmenter), non ?
Pas bête, je ne vois pas la nécessité d’impliquer P(), Q() ou Qt. Le but est d’équilibrer les quantités pondérées n’ayant pas atteint leur maximum tant qu’il reste des grains à répartir, peu importe leur nombre total ou restant.
Oui pour la première remarque mais cela eut se faire au niveau de la fonction, la boucle sur les «grains» à attribuer est simplissime. C’est juste une question esthétique 
Pour le min/max oui, je me suis emmêlé, et effectivement l’utilisation de P(), Q() ou Qt me chagrinait…
#!/usr/bin/python
Qmin=[1000,10000,10000,10000,0]
Qmax=[2000,13000,100000000000000000,10000000000000000,100000000000000000]
P=[1,50,100,100,200]
T=200000
g=100
n=len(Qmin)
Q=[0]*n
def f():
s=1
res=-1
for i in range(n):
if(Qmin[i]>0) and (Q[i]/Qmin[i] < s):
res=i
s=Q[i]/Qmin[i]
if (res >=0):
return(res)
s=Q[0]/P[0]
for i in range(n):
if (Q[i]<Qmax[i]) and (Q[i]/P[i]<=s):
res=i
s=Q[i]/P[i]
return(res)
for i in range(0,T,g):
res=f()
if (res >= 0):
Q[res]=Q[res]+g
print(Q)
Le résulltat n’est pas si mal…
En comparant les résultats de nos deux algorithmes respectifs avec les mêmes jeux de paramètres, j’ai vu que le mien ne donnait pas le résultat attendu dans au moins un cas particulier (un rapport Min/P grand devant les autres fait classer la partition en minimum dès le début alors qu’au final les autres atteignent leur maximum et qu’il reste de l’espace). Je vais essayer de corriger ça…
EDIT
Mon algorithme précédent était basé sur une extrapolation qui n’est hélas pas valide dans tous les cas, donc je l’abandonne. L’approche systématique du tien est plus fiable. Par contre je n’aime pas l’allocation de quantums individuels et l’introduction d’une granularité pour limiter leur nombre.
En considérant que chaque quantité est une fonction d’une variable x arbitraire homogène à Q/P égale à
- Min si P*x < Min
- Max si P*x > Max
- P*x si Min < P*x < Max
alors la somme des quantités est une fonction de x monotone affine par intervalle dont on peut déterminer les points d’inflexion. Leurs abscisses sont les ratios Min/P et Max/P qui sont connus. Il devrait suffire de les ordonner par ordre croissant et calculer successivement l’ordonnée de chaque point. Cela fait, il reste à déterminer entre les ordonnées de quels points d’inflexion se situe la quantité totale, et l’abscisse correspondante permet ensuite de déterminer pour chaque quantité si elle est au minimum, linéaire ou au maximum.
Petit diagramme illustratif :
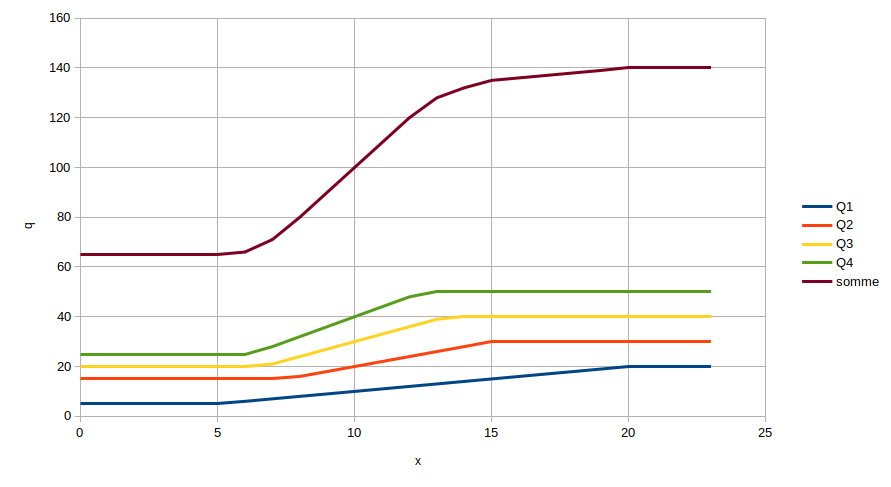
Hum, la notion de points d’inflexion pour une affine par morceaux est douteuse, tu veux parler des segments où la courbe traverse la droite correspondante. Les questions sont donc:
- Y’en a-t-il toujours? [en fait non)
- Ils ne sont pas uniques car c’est en fait tout un segment. Donc lequel prendre?
- Est-il évident que ça correspond à une solution optimale?
En fait je ne comprends pas trop ton schéma. Je le verras comme suit:
Abscisse: quantité x qui va de 0 à 1
Ordonnée: Pour chaque i, Fi(x) = min(max(Qmin(i), x*P(i)*Qtotalmax),Qmax(i))
et F(x) = somme Fi(x).
Tu prends x tel que F(x)=Q la mémoire à attribuée.
Ta fonction est croissante, affine par morceaux et va de 0 à somme des Qmax ou infini, donc Q a un antécédent (si Q >= somme des Qmax(i)). C’est celui là qui t’intéresse. Il ne doit pas être trop mal et pas trop difficile à calculer…
Voila ce que ça donne:
#!/usr/bin/python Qmin=[1000,10000,10000,10000,0] T=200000 Qmax=[2000,13000,T,T,T] P=[1,50,100,100,200] n=len(Qmin) Q=[0]*n Pt=0 for p in P: Pt=Pt+p Qt=0 for q in Qmax: Qt=Qt+q def f(i,x): return(min(Qmax[i],max(x*P[i]/Pt,Qmin[i]))) def ft(x): s=0 for i in range(n): s=s+f(i,x) return(s) a=0 b=Qt delta=10 while(b-a > delta): x=(a+b)/2 if (ft(x)>T): b=x else: a=x Q=[round(f(i,x),0) for i in range(n)] print(Q)
Les résulats entre les deux algorithmes sur un exemple:
$ python repartition2.py [1000, 13000, 46498.0, 46498.0, 92996.0] $ python repartition.py [1000, 13000, 46500, 46500, 93000]
La complexité est pour le premier en T/g n et pour le second en Tln(T)*n donc moins bon que le premier (ce qui est normal, un glouton est moins bien mais efficace).
Je veux parler des points de cassure de la courbe, autrement dit des points de jonction entre les segments.
En effet il y a les cas limites où Min=0 ou Max=infini. Ça ne devrait pas changer fondamentalement les choses, il faut voir à l’implémentation.
Les seuls cas de solution x multiple sont sur les segments plats, quand toutes les quantités sont au min ou au max donc quel que soit x dans cet intervalle le résultat est le même.
Si je ne me suis pas encore vautré comme avec les précédents algorithmes, ça devrait donner le même résultat que ton algorithme granulaire qui est supposé optimal jusqu’à preuve du contraire.
Comme je l’ai écrit, j’ai choisi arbitrairement x homogène à Q/P et l’intervalle pertinent (inconnu au départ) dépend des valeurs d’entrée Min[], Max[] et Qt mais n’est pas important.
Qu’est-ce que Qtotalmax et pourquoi l’introduis-tu dans la formule ?
L’échelle de x est arbitraire, donc n’importe quelle constante strictement positive convient. J’ai choisi 1.
C’est exactement ça, et ce que mon diagramme illustre.
Qu’est-ce que tu veux dire ? Mes cours de math son très loin.
Merci pour le script, je regarde ça.
x n’existe que si f(1)> =Q quantité fournie, donc pour cela il faut que x=1 alloue les maximums possible. Qtotalmax est la somme de ces maximums. Concretement lorsque Qmax[i] n’est pas donné, on prend un Qmax[i] grand ou encore Qmax[i]=Q.
Il existe x tel que f(x)=Q
Si je comprends bien ton script procède par dichotomie.
b=Qt delta=10
Pourquoi avoir choisi ces valeurs ?
La complexité est pour le premier en T/g*n et pour le second en T*ln(T)*n
D’où vient le facteur T pour le second ? Je ne le vois pas dans le script.
PS: attention à * qui peut être interprété comme une balise italique par le forum.
